Recordemos que Z es el conjunto formado por todos los números enteros, tanto positivos como negativos, y el 0.
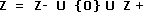
Sabemos, además, que la multiplicación es una suma abreviada donde se repite un sumando, y tiene como elementos a factores y producto.
Distintas situaciones
En la multiplicación de enteros, podemos distinguir tres posibles situaciones, de acuerdo al signo de sus factores:
– Que los dos factores sean enteros positivos.
– Que los dos factores sean enteros negativos.
– Que uno de los factores sea entero positivo y el otro, entero negativo.
Analizaremos lo que sucede en cada caso.
Dos factores son enteros positivos
En este caso, surge de inmediato la pregunta: ¿Qué signo tiene el producto?
Descubramos lo que sucede, resolviendo, por ejemplo:
2 · 3
(No olvides que los enteros positivos no llevan escrito su signo).
En nuestro ejercicio tenemos 2 veces el entero positivo 3. Esta multiplicación es igual a la que hemos resuelto en los números cardinales, donde:
2 · 3 = 6
Si multiplicamos dos enteros positivos, obtendremos un producto positivo.
Podemos comprobarlo utilizando la recta numérica:
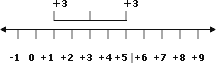
Un factor positivo por un factor negativo
En este caso, nuevamente nos preguntamos: ¿cuál será el signo del producto?
Siempre es un entero negativo.
Observemos el siguiente ejemplo:
3 · -4 = equivale a decir 3 veces -4
En la recta numérica, queda así:
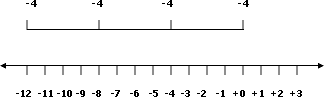
El producto de 3 · -4 = -12
Y ¿cuánto será -5 · 2 ?
Es igual a decir 2 veces -5, ya que aplicamos la propiedad de la conmutatividad.
Graficándolo en la recta numérica queda:
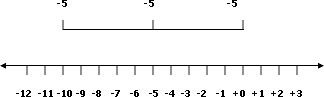
Nuestro producto es -10
El producto de dos enteros negativos
Resolvamos, por ejemplo:
-4 · -1
Primero, aplicaremos paréntesis para dejar afuera el signo – del 4.
En su lugar colocaremos el inverso aditivo que es 4, un entero positivo. Así:
– ( 4 · -1 )
El producto del interior del paréntesis es -4, porque multiplicamos un entero positivo y un entero negativo. Nos queda:
– ( -4 )
Como hay un signo negativo solo, fuera del paréntesis, tendremos que colocar el inverso aditivo del número que está adentro. El inverso aditivo de -4 es 4.
Entonces:
-4 · -1 = 4
Comentarios
Publicar un comentario